有了前面的数据结构基础，这一讲开始，我们谈点较深入的数据结构知识。本讲，我们先来谈谈"树"，建立"树"的基本概念与基本的处理方式。



　　树是一种重要的非线性数据结构，直观地看，它是数据元素（在树中称为结点）按分支关系组织起来的结构，很象自然界中的树那样。树结构在客观世界中广泛存在，如人类社会的族谱和各种社会组织机构都可用树形象表示。树在计算机领域中也得到广泛应用，如在编译源程序如下时，可用树表示源源程序如下的语法结构。又如在数据库系统中，树型结构也是信息的重要组织形式之一。一切具有层次关系的问题都可用树来描述。



一、树的概述



　　树结构的特点是：它的每一个结点都可以有不止一个直接后继，除根结点外的所有结点都有且只有一个直接前趋。以下具体地给出树的定义及树的数据结构表示。



　　（一）树的定义



　　树是由一个或多个结点组成的有限集合，其中：

　　⒈必有一个特定的称为根(ROOT)的结点；

　　⒉剩下的结点被分成ｎ>=0个互不相交的集合T1、T2、......Tn，而且， 这些集合的每一个又都是树。树T1、T2、......Tn被称作根的子树(Subtree)。



　　例如，一个集团公司，可以描述如下:

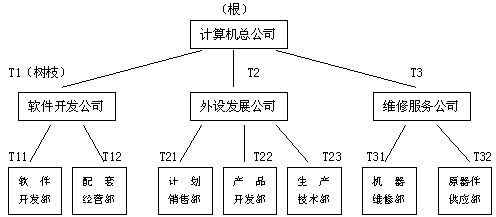
　　它很象一株倒悬着的树，从树根到大分枝、小分枝、直到叶子把数据联系起来，这种数据结构就叫做树结构，简称树。



　　树中每个分叉点称为结点，起始结点称为树根，任意两个结点间的连接关系称为树枝，结点下面不再有分枝称为树叶。结点的前趋结点称为该结点的"双亲"，结点的后趋结点称为该结点的"子女"或"孩子"，同一结点的"子女"之间互称"兄弟"。



　　（二）树的表示



　　树中每个结点的内容分两部分表示：⒈结点的性质；⒉结点的指针域。

　　结点的性质：描述结点的必要数据。

　　结点的指针域：指向结点的每一个孩子。

　　指针域采用多重链表，又分为不定长度结点的多重链表与固定长度结点的多重链表。

　　不定长度结点的多重链表表示树时，每个结点的指针域个数等于该结点的孩子的个数，其形式如下：

DATA

CHILD1

CHILD2

……

CHILDn

　　每个指针域指向一个孩子，这样虽然不浪费空间，但由于结点长度不等，将给存储分配造成困难，给各种运算带来极大不便。

　　固定长度结点的多重链表表示树时，树中每个结点的指针域个数都相等于树中结点的最大度数，也就是说，不论结点的孩子多少，其长度均取最大长度。这样长度划一，处理问题简单方便，但对存储空间浪费很大。

　　为了寻求一种恰当的树的存储表示方法，我们将讨论一种称之为二叉树的树型结构。



二、二叉树



　　二叉树是一种十分重要的树型结构。它的特点是，树中的每个结点最多只有两棵子树，即树中任何结点的度数不得大于２。二叉树的子树有左右之分，而且，子树的左右次序是重要的，即使在只有一棵子树的情况下，也应分清是左子树还是右子树。



　　（一）定义



　　二叉树是结点的有限集合，这个集合或是空的，或是由一个根结点和两棵互不相交的称之为左子树和右子树的二叉树组成。

　　图2列出了二叉树的五种基本形态。

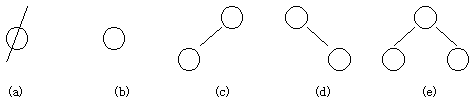
　　　　　　　　　　　　　　　　　　　　　 图 2



　　(a)为空二叉树；(b)只有一个结点的二叉树；(c)只有左子树的二叉树；(d)只有右子树的二叉树；(e)左右完全的二叉树。



　　（二）满二叉树



　　一棵深度为K的满二叉树，是有2K-1个结点的深度为K的二叉树。2K-1个结点是二叉树所能具有的最大结点个数。图3所示为一棵深度为４的满二叉树。

　　　 　　　　 　　 　　　　　　 　　

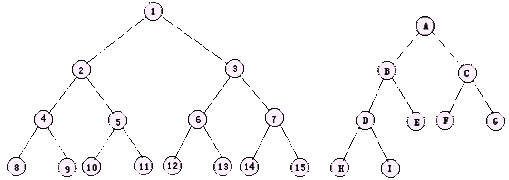
　　　　　　　　　　　　　　　图 3 　　　　　　　　　　　　　　图 4　



　　（三）完全二叉树



　　对满二叉树，从第一层的结点(即根)开始，由下而上，由左及右，按顺序结点编号，便得到满二叉树的一个顺序表示。据此编号，完全二叉树定义如下：一棵具有ｎ个结点，深度为K的二叉树，当且仅当所有结点对应于深度为K的满二叉树中编号由１至ｎ的那些结点时，该二叉树便是完全二叉树。图4是一棵完全二叉树。



　　（四）二叉树的存储



　　二叉树一般采用双重链表作为其存储结构，表中每个结点都有三个域：数据域DATA、左指针域LCHILD和右指针域RCHILD。其中指针域LCHILD和RCHILD分别指向其左孩子和右孩子。如图5所示。

　　　　　　　　　　　　　　　　 图5 　二叉树结点的结构形式



三、二叉树的遍历



　　遍历是对树的一种最基本的运算，所谓遍历二叉树，就是按一定的规则和顺序走遍二叉树的所有结点，使每一个结点都被访问一次，而且只被访问一次。由于二叉树是非线性结构，因此，树的遍历实质上是将二叉树的各个结点转换成为一个线性序列来表示。



　　设L、D、R分别表示遍历左子树、访问根结点和遍历右子树， 则对一棵二叉树的遍历有三种情况：DLR（称为先根次序遍历），LDR（称为中根次序遍历），LRD
（称为后根次序遍历）。



　　（一）先根次序遍历的递归定义



　　若二叉树为空，则返回；否则，依次执行以下操作：

　　⒈访问根结点；

　　⒉按先根次序遍历左子树；

　　⒊按先根次序遍历右子树；

　　⒋返回。



　　例1 图6为表示表达式 （ａ＋ｂ×（ｃ－ｄ））－ｅ/ｆ的二叉树。

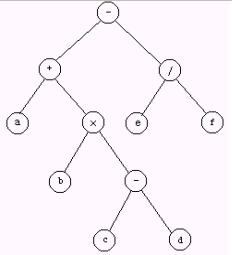
　　　　　　　　　　　　　　　　　　　　　图 6



　　先序遍历此树时，首先访问根结点，得到字符"－"。继而访问结点"－"的左子树，按递归定义，先访问子树的根结点，得到字符"＋"。类推访问结点"＋"的左子树，此时只有叶子。得到叶子"ａ"后，访问叶子"ａ"父结点的右子树，得到右子树的根结点字符"×"。再访问结点"×"的左子树，得到叶子字符"ｂ"后，访问字符"ｂ"父结点的右子树，得到右子树根结点字符"－"，……。先序遍历完整棵树，得到序列为：
－＋ａ×ｂ－ｃｄ/ ｅｆ

　　这就是表达式的前缀表示或称波兰表示。



　 （二）中根次序遍历的递归定义



　　若二叉树为空，则返回；否则，作如下操作：

　　⒈按中根次序遍历左子树；

　　⒉访问根结点；

　　⒊按中根次序遍历右子树；

　　⒋返回。



　　中序遍历图6二叉树时，引入栈，先将根结点字符"－"入栈，按定义访问根结点的左子树，遇到子树的根结点字符"＋"入栈，访问结点"＋"的左子树，到达叶子字符"ａ"，则字符"ａ"为第一个访问的结点。接着，将栈顶字符出栈，访问子树根结点字符"＋"。继而访问其右子树，方法同上，子树根结点"×"入栈，……。这样，中序遍历完整棵树后，得到的序列为：
ａ＋ｂ×ｃ－ｄ－ｅ/ ｆ

这就是表达式的中缀表示。



　 （三）后根次序遍历的递归定义



　　若二叉树为空，则返回；否则，作如下操作：

　　⒈按后根次序遍历左子树；

　　⒉按后根次序遍历右子树；

　　⒊访问根结点；

　　⒋返回。

　　对图6二叉树，后序遍历后得到的序列为： 　 ａｂｃｄ－×＋ｄｆ/ －

　　这就是表达式的后缀表示或称表达式的逆波兰表示。逆波兰表示的表达式的优点在于它得到的是不加括号的表示式，但从表示式中确能确定表达式的运算先后顺序。故在源程序如下编译表达式值的处理等方面的应用中经常用到。