趣谈数据结构(四)
http://www.mydrs.org 7/4/2001 大榕树
本次趣谈数据结构,我们想与大家共同探讨一下迭代与递推。在计算机数值程序设计中,迭代与递推是两个重要的基础算法。
一、迭代
许多的实际问题都能转化为解方程F(x)=0的实数解的问题。求根可以直接从方程出发,逐步缩小根的存在区间,把根的近似值逐步精确到要以满足具体实际问题的需要为止,该算法称为迭代。迭代的一般原则可以用一个数学模型来描述,现要求出方程F(x)=0的解:先设F(x)=G(x)-x,则方程F(x)=0可化为x=G(x),
这就产生了一个迭代算法的数学模型:
Xn+1=G(Xn)
从某一个数X0出发,按此迭代模型,求出一个序列:
{X0,X1,X2,X3,……,Xn-2,Xn-1,Xn}
当Xn-Xn-1小于一个特定值(误差许可值)时,X≈Xn-1≈Xn,这时可认定x=G(x)。也就是说,求出的Xn已经可以作为原方程f(x)=0根的近似值了。
设误差许可值为A,则迭代算法的NS图如图1。
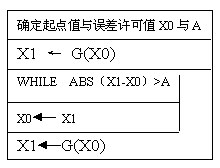
图1 迭代算法NS框图
迭代算法的关键在于确定迭代函数G(x)。确定G(x)时需保证产生的迭代序列{Xn }是否能使两个相邻的数之间的差距越来越小(即两数的差值越靠近误差值,我们称这样的序列为收敛序列),因为只有这样才能使根的存在范围越来越小,从而为根的取得创造条件。
例1 求2的算术平方根(不使用内部函数)。
分析:使用迭代算法来解决这个问题,使用迭代法可以先设X=SQRT(2)-1,则求2 的算术平方根的近似值就可以转化为求X(X+2)=1的正根。列出等价方程X=1/(X+2),
以1/(X+2)为迭代函数,以0为初始近似值X0,误差值设定为0.0000001, 则程序可写成:
program ex11_7;
const a=0.0000001;
var x0,x1,X:real;
begin
x0:=0;x1:=1/(x0+2);
while abs(x1-x0)>a do
begin
x0:=x1;x1:=1/(x0+2);
end;
x:=x1+1; {将X1的值转为2的算术平方根}
writeln('sqrt(2)=',x);
end.
程序的输出结果如下:SQRT(2)=1.4142135516E+00
开始时,迭代函数的根的近似值设定在[0,0.5]之间, 由于区间宽度大于给定误差许可值,于是再进行迭代运算,产生下一个区间[0.4,0.5];
其宽度仍然大于误差许可值,再产生下一个区间;……;如此反复,直到区间的宽度小于误差给定值时,则表明在该区间中,任意选择一个数都可以满足根的近似值要求了。为方便起见,取下该区间的边界置作为近似值。这就是迭代算法的一般原则的体现了。
二.递推
对于一个的序列来说,如果已知它的通项公式(即表达位置与位置上的数据的关系的公式),那么,要求出数列中某项之值是十分容易的。但是,在许多情况下,要得到数列的通项公式是很困难的,甚至无法得到。然而,一个有规律的数列的相邻位置上的数项之间通常存在着一定的关系,我们可以借助已知的项,利用特定的关系逐项推算出它的后继项的值,……,如此反复,直到找到所需的那一项为止,这样的方法称为递推算法。
递推算法的首要问题是得到相邻的数据项间的关系(即递推关系)。递推算法避开了求通项公项的麻烦,把一个复杂的问题的求解,分解成了连续的若干步简单运算。一般说来,可以将递推算法看成是一种特殊的迭代算法。
例2 著名的菲波纳葜(Fibonacci)数列,其第一项为0,第二项为1,
从第三项开始,其每一项都是前两项的和。编程求出该数列第N项数据。
分析:按菲波纳葜数列的原则,数列为:
0 1 1 2 3 5 8 13 21 34 55……
无疑地,寻找其项数位置与项值的关系(即通项公式)是非常困难的。而根椐该数列的形成规则,其有一个的公式即"Un=Un-1+Un-2
"表明了相邻的数据项之间的明显关系。因此,可以其作为递推公式,以已知项0与1为起点,逐项产生第3项、第4项、……,直到取得需要的第N项为止。
在其递推算法的语言实现上,可取J、K、P三个变量,分别表示前二项、前一项与当前项,J、K分别取初值0与1。第一次通过递推公式P=J+K得到第三项,并进行移位,即J取K值、K取P值,
为下次递推作准备;……;如此反复,经过N-2次的递推,P就是第N项的值(第1次产生的是3项的值)。
源程序如下:
program ex11_8;
var
n,i,j,k,p:longint;
begin
write('N=');readln(n);
i:=2;j:=0;k:=1;
repeat
inc(i);p:=j+k;j:=k;k:=p;
until i=n;
writeln('F(',n,')=',p);
end.
菲波纳葜数列的递推明确地体现了递推算法程序设计的一般原则,即递推公式取得。
例3 数字三角形。如下所示为一个数字三角形。请编一个程序计算从顶到底的某处的一条路径,使该路径所经过的数字总和最大。只要求输出总和。
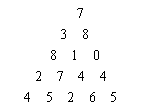 1、 1、
一步可沿左斜线向下或右斜线向下走;
2、 角形行数小于等于100;
3、 三角形中的数字为0,1,…,99;
测试数据通过键盘逐行输入,如上例数据应以如下所示格式输入:
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
分析:此题解法有多种,从递推的思想出发,可以设想,当从顶层沿某条路径走到第I层向第I+1层前进时,我们的选择一定是沿其下两条可行路径中最大数字的方向前进,为此,我们可以采用倒推的手法,设a[i,j]存放从i,j
出发到达n层的最大值,则a[i,j]=max{a[i,j]+a[i+1,j],a[i,j]+a[i+1,j+1]},a[1,1] 即为所求的数字总和的最大值。
源程序如下:
program ex11_9;
var n,j,i:integer;
a:array[1..100,1..100] of integer;
begin
read(n);
for i:=1 to n do
for j:=1 to i do
read(a[i,j]);
for i:=n-1 downto 1 do
for j:=1 to i do
begin
if a[i+1,j]>=a[i+1,j+1] then a[i,j]:= a[i,j]+a[i+1,j]
else a[i,j]:=a[i,j]+a[i+1,j+1];
end;
writeln(a[1,1]);
end.
|



