在趣谈数据结构（四）中，我们了解了迭代与递推。与迭代、递推相对应的算法为递归，本趣谈数据结构，我们就来谈一谈递归算法。



　　递归算法作为计算机程序设计中的一种重要的算法，是较难理解的算法之一。简单地说，递归就是编写这样的一个特殊的过程，该过程体中有一个语句用于调用过程自身（称为递归调用）。递归过程由于实现了自我的嵌套执行，使这种过程的执行变得复杂起来，其执行的流程可以用图1所示。
　　

　 　　　　

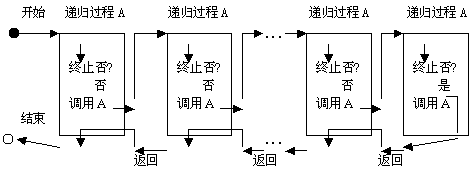
　　　　　　　　　　　　　　　　图1　递归过程的执行流程



从图1可以看出，递归过程的执行总是一个过程体未执行完， 就带着本次执行的结果又进入另一轮过程体的执行，……，如此反复，不断深入，直到某次过程的执行遇到终止递归调用的条件成立时，则不再深入，而执行本次的过程体余下的部分，然后又返回到上一次调用的过程体中，执行其余下的部分，……，如此反复，直到回到起始位置上，才最终结束整个递归过程的执行，得到相应的执行结果。递归过程的程序设计的核心就是参照这种执行流程，设计出一种适合"逐步深入，而后又逐步返回"的递归调用模型，以解决实际问题。



　　利用递归调用程序设计技术可以解决很复杂但规律性很强的问题，并且可以使程序变得十分简短。



例1 利用递归调用手段编程计算N!。



　　分析：根椐数学知识，1!=1，正整数N的阶乘为：N*(N-1)*(N-2)*…*2*1， 该阶乘序列可转换为求N*(N-1)!，而(N-1)!以可转换为(N-1)*(N-2)!，……，直至转换为2*1!，而1!=1。



源程序如下:

program ex11_10;

var

　n:byte;

　t:extended;

procedure find(n:byte);

　begin

　　if n=1 then t:=1

　　else

　　　begin

　　　　find(n-1);t:=t*n;

　　　end;

　end;

begin

　write('N=');readln(n);

　find(n);

　writeln('N!=',t:1:0);

end.



　　在过程find中，当N>1时，又调用过程find，参数为N-1，…，这种操作一直持续到N=1为止。　　例如当N=5时，find(5)的值变为5*find(4)，
求 find( 4)又变为4*find(3)，…，当N= 1时递归停止，逐步返回到第一次调用的初始处，返回结果5*4*3*2*1，即5!。



例2 利用递归调用技术求菲波纳葜数列的第N项。



　　分析：我们已经知道菲波纳葜数列的各数列的产生可用下列公式表示：

　　　　Ｕ1＝０　　Ｕ2＝１ Ｕn＝Ｕn-1＋Ｕn-2 （当n>2时）

　　因此当N大于2时，求第N项值可转化为求第N-1项值与第N-2项值的和； 而求第N-1项又可转化为求N-2项值与N-3项的和，相应地，求N-2项值可转化为求N-3
项值和N-4项值的和；……；如此反复，直至转化为求第1项或第2项值，而第 1项与第2项为已知值1和2。



源程序:

program ex11_11;

var

　n:byte;

　a:array[1..100] of longint;

function f(n:byte):longint;

　var i:longint;

　begin

　　if a[n-1]>0 then i:=a[n-1]

　　else i:=f(n-1);

　　if a[n-2]>0 then i:=i+a[n-2]

　　else i:=i+f(n-2);

　　a[n]:=i;f:=i;

　end;

begin

　write('N=');readln(n);

　fillchar(a,sizeof(a),0);

　a[1]:=1;a[2]:=1;

　writeln('F(',n,')=',f(n));

end.



　　本程序采用了函数递归，函数F的执行比较复杂。函数F由于存在着两次的递归调用，使递归调用产生执行流程的"二叉树"行式，大家可参照图2
来理解这个执行过程。为方便起见，设定N=5，图中的数码表示递归执行的顺序。

　　　　　　　　　　　　　　　　　

　　　　　　　　　　

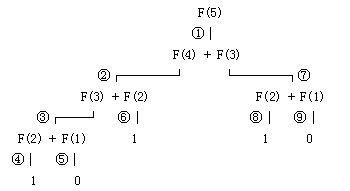
　　　　　　　　　　　　　　　　图2 F函数的"二叉树"执行流程



　　递归调用技术的运用， 是在牺牲计算机内存空间和程序执行速度的基础上得到的。因为在递归调用的执行过程中，系统必须花费时间与空间以栈的方式记下每次调用的返回位置地址及每一次过程执行的中间结果，以便当递归调用终止条件成立时，能沿着"逐步深入"的路线"逐步返回"，取得这些数据，最终准确地回到初始调用处。比如，同是解决菲波纳葜数列问题的程序，使用递推就比使用递归算法设计的程序执行速度快了许多。



　　当一个问题蕴含着递归关系且结构比较复杂时，采用一般的算法，不仅给程序的设计带来许多困难，而且也会给设计出的程序带来篇幅大、可读性差的缺点，这时采用递归调用技术来设计程序则会带来相反的效果。



例3　相传在古印度的布拉玛婆罗门圣庙的僧侣在进行一种被称为汉诺塔的游戏，其装置是一块铜板，上面有三根杆（编号A、B、C），A杆上自下而上、由大到小按顺序串上64个金盘（如图3）。游戏的目标是把
A杆上的金盘全部移到C杆上，并仍原有顺序叠好。条件是每次只能移动一个盘，并且在每次移动都不允许大盘移到小盘之上。现要求利用递归调用技术给出N个盘从A杆移到C杆的移动过程。

　　　　　　　 　　　　　　

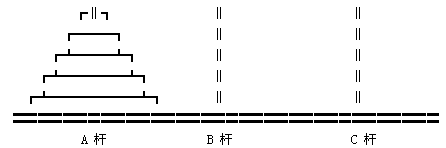
　　　　　　　　　　　　　　　　　　图3 N阶汉诺塔



　　分析：这个移动过程很复杂与烦琐，但规律性却很强。使用递归调用技术来解决这个移动过程，先得找到一个递归调用模型。想要得到汉诺塔问题的简单解法，着眼点应该是移动A杆最底部的大盘，而不是其顶部的小盘。不考虑64个盘而考虑N个盘的一般情况。要想将A杆上的N个盘移至C杆，我们可以这样设想：



　　1.以C盘为临时杆，从A杆将1至N-1号盘移至B杆。

　　2.将A杆中剩下的第N号盘移至C杆。

　　3.以A杆为临时杆，从B杆将1至N-1号盘移至C杆。



　　我们看到，步骤2只需移动一次就可以完成；步骤1与3的操作则完全相同， 唯一区别仅在于各杆的作用有所不同。这样，原问题被转换为与原问题相同性质的、规模小一些的新问题（图4）。即：
HANOI(N,A,B,C) 可转化为 HANOI(N-1,A,C,B)与 HANOI(N-1,B,A,B)



　　其中HANOI中的参数分别表示需移动的盘数、起始盘、临时盘与终止盘， 这种转换直至转入的盘数为0为止，因为这时已无盘可移了。 这就是需要找的递归调用模型。



　　　　　　

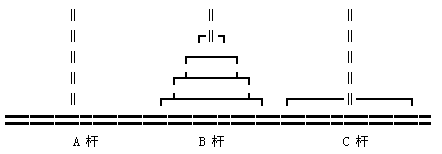
　　　　　　　　　　　　　　　　　图4 N-1阶汉诺塔



源程序如下:

program ex11_12;

var

　a,b,c:char;

　n:byte;

procedure hanoi(n:byte;a,b,c:char);

　begin

　　if n>0 then

　　　begin

　　　　hanoi(n-1,a,c,b);

　　　　writeln('Move ',a,' to ',c);

　　　　hanoi(n-1,b,a,c);

　　　end;

　end;

begin

　a:='A';b:='B';c:='C';

　write('N=');readln(n);

　hanoi(n,a,b,c);

end.



　　如果说例1与例题的无法体现递归算法的独特优点，那么，例3的解法则很能说明问题，因为一般的算法是很难解决这个问题的，而过程HONOI只用了4个语句就解决这个难题。不过要说明的是，按照汉诺塔的移动原则，将N个盘从A杆移动到C
杆需要移动盘的次数是 2 的 N 次幂减 1 ， 那么 64 个盘移动次数就是18446744073709511615，近19亿亿次。这是一个天文数字，即使一台功能很强的现代计算机来解汉诺塔问题，恐怕也需要很长的时间，因此要想得到结果，在运行程序时，输入的N可不能太大。据说布拉玛婆罗门圣庙的僧侣声称，
汉诺塔游戏结束就标志着世界末日的到来，现在看来确实是有道理的。因为如果每秒移动一次，64个盘则大约需近5800亿年，而据科学家以能源角度推算，太阳系的寿命只不过150
亿年而已。